8.6. chatGPT

Open AI’s chatGPT combines an Autoregressive Large Language Model (AR LLM) with the concept of Reinforcement Learning with Human Feedback (RLHF). The applied AR LLM is GPT-3, as introduced in [BMR+20]. The combination of a AR LLM with RLHF has been introduced in InstructGPT ([OWJ+22]).

In general, RLHF can solve the problem, that in Neural Networks the model is trained such that a loss-function is minimized. However, minimization of a loss function often is not aligned with what is prefered/expected by the user. Depending on the task, users may assess the output of a model B better than the output of another model A, even though model A has a smaller loss-value. If an answer to a question, a generated text, a text-summarisation etc. is good can only be assessed subjectively by humans.

RLHF is a method to fine-tune Neural Networks with human preferences - instead of minimizing a loss-function for fine-tuning. RLHF enables a LLM to align a model trained on a corpus of text data to human preferences.

The entire training process can be described by 4 phases:

1. Pretraining of a Autoregressive Large Language Model (AR LLM), typically from a large corpus of unlabeled training data

2. Gathering data, which contains prompts, the corresponding LLMs output and a human rating of this output.

3. Use this human rated prompt-output pairs to train a reward model (usually also a LLM).

4. This model provides the reward for fine-tuning the AR LLM with reinforcement learning.

Below, these 4 phases of GPT-training are described in more detail.

8.6.1. Concept of Reinforcement Learning

In supervised Machine learning a set of training data \(T=\lbrace (\mathbf{x}_i,r_i) \rbrace_{i=1}^N\) is given and the task is to learn a model \(y=f(\mathbf{x})\), which maps any input \(\mathbf{x}\) to the corresponding output \(y\). This type of learning is also called learning with teacher. The teacher provides the training data in the form that he labels each input \(\mathbf{x}_i\) with the corresponding output \(r_i\) and the student (the supervised ML algorithm) must learn a general mapping from input to output. This is also called inductive reasoning.

In reinforcement learning we speak of an agent (the AI), which acts in an environment. The actions \(A\) of the agent must be such that in the long-term the agent is successful in the sense that it approximates a pre-defined goal as close and as efficiently as possible. The environment is modeled by it’s state \(S\). Depending on it’s actions in the environment the agent may or may not receive a positive or negative reward \(R\). Reinforcement learning is also called learning from a critic, because the agent trials different actions and sporadically receives feedback from a critic, which is regarded by the agent for future action decisions.

Reinforcement Learning refers to Sequential Decision Making. This means that we model the agents behaviour over \(time\). At each discrete time-step \(t\) the agent perceives the environment state \(S_t\) and possibly a reward \(R_t\). Based on these perceptions it must then decide for an action \(A_t\). This action influences the state of the environment and possibly triggers a reward. The new state of the environment is denoted by \(S_{t+1}\) and the new reward is denoted by \(R_{t+1}\). In the long-term the agents decision-making-process must be such, that a pre-defined target-state of the environment is approximated as efficiently as possible. The proximity of a state \(s\) to the target-state is measured by an utility function \(U(s)\).

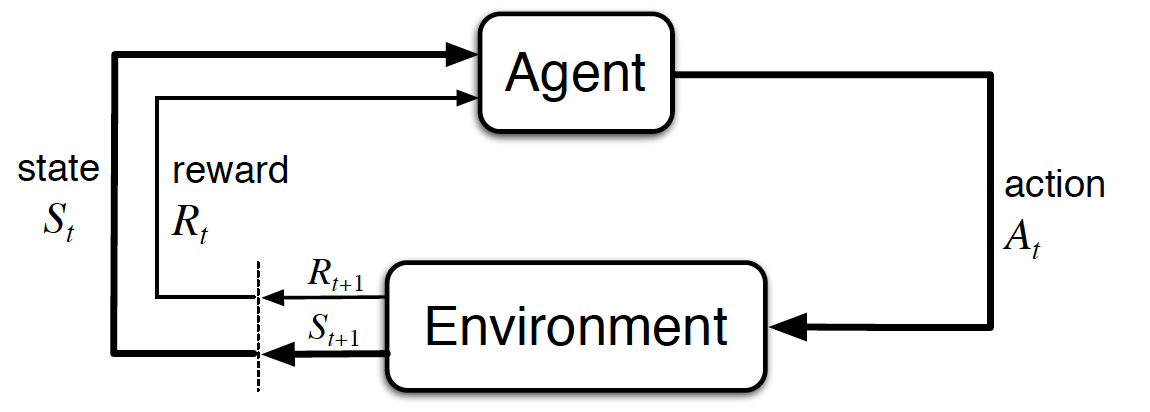
Fig. 8.34 Interaction of an agent with it’s environment in a Markov Decision Process (MDP). Image source: [SB18].

8.6.1.1. Example: Non-deterministic Navigation

Navigation or similarly pathfinding can be solved by the A*-algorithm, if the environment is deterministic. This means that given the current state \(s_t\) and a selected action \(a_t\), the successive state \(s_{t+1}\) can uniquely be determined. In a non-deterministic there exist different possible successive states for a given state-action-pair. In such non-deterministic environments Reinforcemt Learning can be applied to learn an optimum policy. This policy defines for each state the action, which is best, in the sense that the expected future cumulative reward (the utility) is maximized.

In the example depicted below the task is to find the best path from the field \(Start\) to the field in the upper right corner. The possible actions of the agent are to move upwards, downwards, right or left. The environment is observable in the sense that the agent knows it’s current state. However, the environment is non-deterministic because for a known state-action-pair different successive states are possible. For this uncertainty the following probabilities are assumed to be known:

• Probability that state in the selected direction is actually reached is \(P=0.8\).

• Probability for a \(\pm 90°\) deviation is \(P=0.1\) for each.

If selected direction hits a wall, the agent remains in it’s current state. A reward of \(r_t=1\) is provided, if \(a_t\) terminates in field \((4/3)\) (the upper right corner) and a reward of \(r_t=-1\) is provided if \(a_t\) terminates in field \((4/2)\). For any other action the reward (cost) is \(r_t=-0.04\).

Fig. 8.35 Image source: [RN10]: Pathfinding in a non-deterministic environment

For this pathfinding scenario, the optimum policy, learned by the RL agent may look like in the picture below. The policy is defined by the arrows in the states. These arrows determine in each state the action to take in order to maximize the expected future cumulative reward.

Fig. 8.36 Image source: [RN10]: Optimum policy learned by the RL agent

8.6.2. Reinforcementlearning with Human Feedback (RLHF) in chatGPT

8.6.2.1. Step 1: Pretraining of AR LLM

In this step the GPT-3 AR-LLM is pretrained in a self-supervised manner as described in the transformer section. As depicted in the image below, in addition to the self-supervised AR-LLM pretraining optionally supervised fine-tuning can be applied in this step, e.g. openAI applied user generated texts for this fine-tuning.

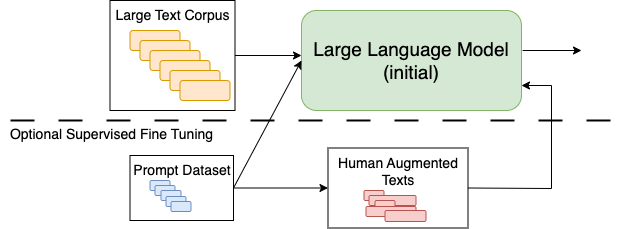
Fig. 8.37 Pretraining with unlabeled texts (next word prediction) and optional fine-tuning with prompts and user augmented texts. In chatGPT the LLM is GPT-3.

8.6.2.2. Step 2: Gathering data for Training the Reward Model

In this step a training dataset of (prompt/generated-text)-pairs must be generated. For this a set of prompts is sampled from a given prompt-dataset. For example openAI gathered such a prompt-datset from prompts, which have been submitted by users to the chatGPT API. The sampled prompts are passed to the initial LLM from step 1 in order to get the (prompt/generated-text)-pairs.

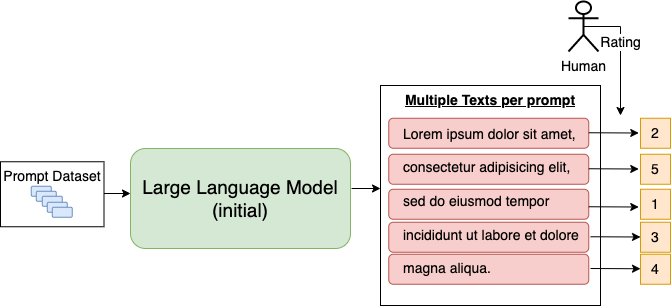
Fig. 8.38 For each prompt multiple LLM outputs are generated. These output texts are rated by a user.

8.6.2.3. Step 3: Training the Reward Model

In this step the goal is to generate a model, which receives texts and returns a scalar, which reflects the user’s preference (assessment) of the input texts. This model is called reward model or preference model. The scalar output of the model is applied as the reward-value in the reinforcement learning based fine-tuning of the next step. The scalar output for the text input can either be generated in a single end-to-end network or in multiple stages. For example a common approach is to first use a LLM to produce a ranking of multiple output-texts (generated by different LLMs) for a common input prompt. In a second step another ML-algorithm transforms the ranking into a scalar reward. This two-step-approach is preferable, since it is easier for the human annotators to rank documents, than to assign a scalar reward value (personal-bias).

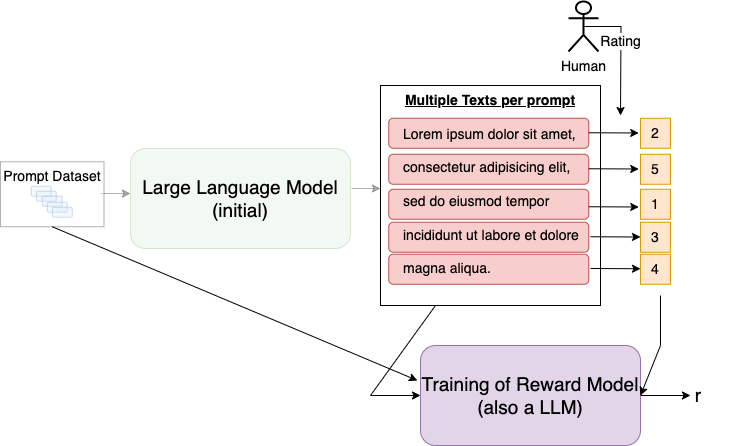
Fig. 8.39 Each generated pair of (generated text, scalar reward from human assessement) constitutes a datasample for supervised training of the reward model.

8.6.2.4. Step 4: Fine Tune LLM with Reinforcement Learning

In this step we first copy the initial LLM with weights \(\Theta_I\) from step 1. We keep one copy in its initial state (initial LLM). The other copy is going to be fine-tuned (fine-tuned LLM). The weights of the fine-tuned model are denoted by \(\Theta_F\). Initially

\[ \Theta_F := \Theta_I. \]

Only the weights \(\Theta_F\) of the fine-tuned LLM will be adapted, the weights \(\Theta_I\) of the initial LLM will remain unchanged.

The setting for reinforcement learning can be defined as follows:

• The state of the RL-Agent is the prompt \(x\).

• The action is the output sequence \(y\), generated for the given prompt \(x\).

• The strategy \(\pi_{\Theta_F}(y \mid x)\) is defined by the fine-tuned LLM with adaptable parameters \(\Theta_F\). It defines for each prompt \(x\) a probability distribution over possible text-sequences \(y\).

Prompts \(x\) from the prompt-dataset are passed to both, the initial LLM and the fine-tuned LLM. For a given prompt \(x\) the output of the initial LLM is \(y_I \sim \pi_{\Theta_I}(y \mid x)\) and the output of the fine-tuned LLM is \(y_F \sim \pi_{\Theta_F}(y \mid x)\).

The output \(y_F\) of the fine-tuned LLM is passed to the input of the trained reward-model, which calculates a reward \(r(y_F \mid x)\). The task of the RL-algorithm is to adapt the weights \(\Theta_F\) of the fine-tuned LLM, such that a utility function \(J\) is maximized. This maximisation is realized by a Policy Gradient RL technique, i.e. the weights \(\Theta_F\) are iteratively adapted into the direction of the gradient of the utility function \(\nabla J(\Theta_F)\):

\[ \Theta_F := \Theta_F + \nabla J(\Theta_F). \]

The utility function \(J(\Theta_F)\) certainly contains the rewards \(r(y_F \mid x)\), since the goal is to adapt the LLM into the direction of the user preferences. However, there is a second component, which is the negative Kullback-Leibler-Divergence between the probability distributions \(\pi_{\Theta_F}(y \mid x)\) and \(\pi_{\Theta_I}(y \mid x)\) of the fine-tuned LLM and initial LLM, respectively:

\[ J = r(y_F \mid x) - \lambda_{KL} D_{KL}( \pi_{\Theta_F}(y \mid x) \mid \mid \pi_{\Theta_I}(y \mid x)). \]

The KL divergence term penalizes the output of the fine-tuned LLM from moving to far away from the initial pretrained LLM. It has been shown that without this penalty the fine-tuned model tends to output non-coherent text snippets.

For Reinforcement Learning usually Proximal Policy Optimization (PPO)([SWD+17]) is applied. It updates the parameters \(\Theta\) per batch of training data (input prompts).

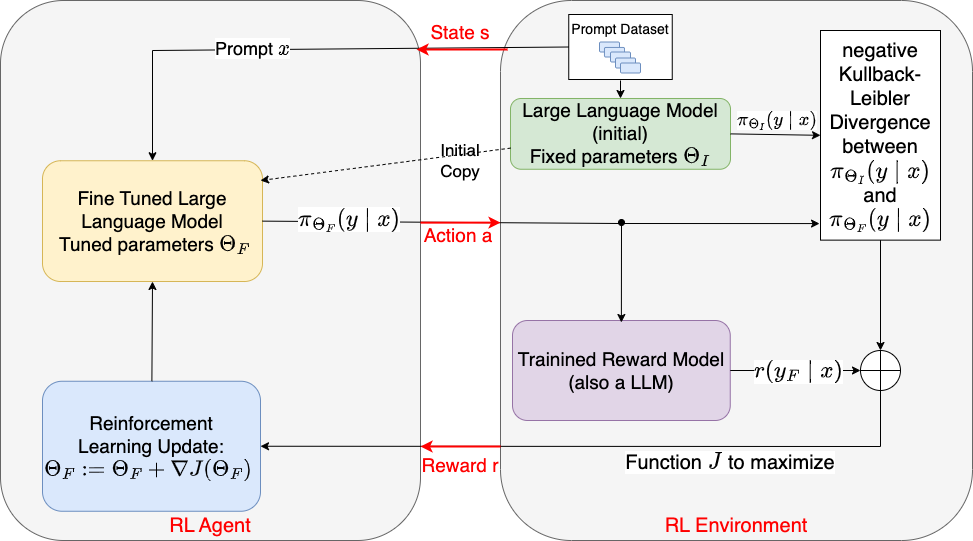
Fig. 8.40 Update weights of LLM with Reinforcement Learning. The utility function, which is maximized in the RL algorithm is a combination of the estimated reward (user preference) and the negative Kullback-Leibler-Divergence, which is a measure for the similiarity between the fine-tuned LLMs output-distribtution and the initial LLMs output distribution.